「周波数」を手っ取り早く理解する
音楽に触れていると、たびたび「周波数」とか「周波数特性」あるいは「高域」「低域」という言葉が出てきます。
このページではこれら「周波数」うんたらを手っ取り早く理解するための説明を試みます。。
周波数がわかると音楽を視覚的に解釈する手立てが増えますし、音楽やオーディオ記事を読んだ時にわかる内容がぐっと広がると思います。
分かりやすさを考慮して、いろいろ都合よい省略をしています。
また1Hzや15Hzが出てきますが、人間が聴けるのは20Hz以上なので、あくまで例として低い周波数を出しています。
1.低い音と高い音
音は空気の振動ですし、オーディオ機器ではその振動が電気の振動に変換されています。
この振動の時間変化は図1のようにしばしば波の形で表現されます。
音には低い音と高い音があります。
例えばバスドラやベースが出すのは低い音、ヴォーカルのサシスセソ音は高い音です。もちろん真ん中あたりの音もあります。
図1-1 
図1-2 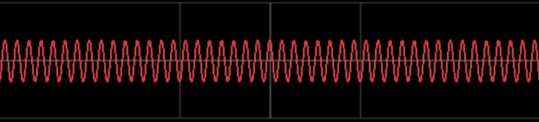
横軸を時間としたとき、上の図1-1と図1-2では、図1-1よりも図1-2のほうが速い振動です。
なぜなら同じ時間の中で山谷を繰り返す数が図1-2のほうが多いからです。
人の耳には、図1-1は低い音、図1-2は高い音に聴こえます。
つまり、音が低いか高いかは空気や電気の振動の速さによって決まっています。
2.周波数とは
この振動の速さを数値化したものが周波数です。
図2-1 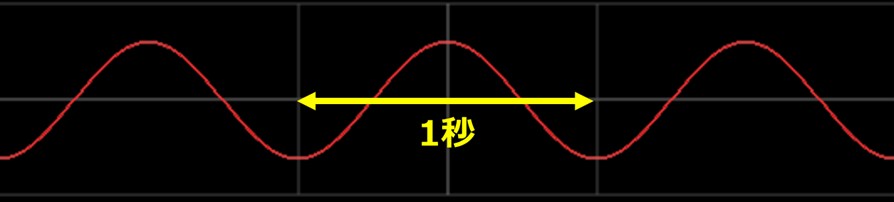
図2-1の黄色矢印の区間が1秒だった時、この区間に赤い波は1回分あります。
矢印の左端で谷があり、右端でまた谷になっているから1回分です。
これが周波数1Hz(ヘルツ)と定義されます。
図2-2
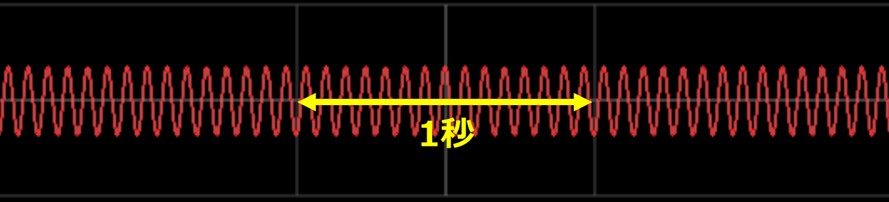
図2-2の波は15Hzです。黄色い矢印の区間に15回振動があります。
人間が聞けるのは20Hz〜20kHzと言われてます。これは1秒間に20回〜2万回の空気振動です。
人間ってすごいですね。でも犬はもっと高い音まで聞けるそうです。
ただ、2万Hzを図に描こうと思うと、もっともっと1秒を長くとらないといけないですね。
3.周波数を描く
この周波数を図で表現したいのですが、いちいち波を描くのは面倒ですし、
描いたとしても図2-2が何Hzか瞬時にわかる人はいないでしょう。それにもっと高い周波数、それこそ2万Hzになるともう描いてられない。
そこで画期的な簡単な表現方法が発明されました。これが周波数領域表示です。(単純に周波数表示と言ったり、単純に「周波数見て」とか言ったりもします。)
図3-1
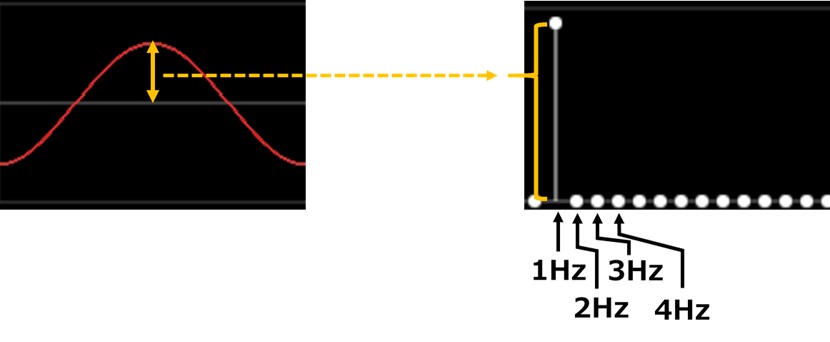
図3-1の左側がこれまで出していた1Hzの波形(時間領域と呼びます)、そして右側が周波数領域です。
周波数領域では、時間領域のようにいちいち波を描くのではなく、
横軸に周波数を取り、該当する周波数の場所に時間領域の波の幅をすっと棒で記入します。
つまりたった1本の棒で波を表現するのです。とても簡単に描けて見やすいですね。
図3-2 
図3-3 
図3-2右は1Hzを、図3-3右は15Hzを周波数領域に描いたものです。
周波数領域なら、例え20kHz(2万回振動/秒)であっても、横軸を長くとって棒を1本描くだけで表現できてしまうわけです。
4.音楽や声は複数の周波数で出来ている
音は(音楽や声以外も)たいてい複数の周波数の波が重なって出来ています。図4-1のような感じ。
図4-1 
図4-1は上の図3-2(1Hz)と図3-3(15Hz)が重なった波です。時間領域でも1Hzと15Hzが見えますが、周波数領域ならより分かりやすい。
図4-2 
図4-2はもっといろいろな周波数の波をいろいろな大きさで重ねてみました。
時間領域ではなんとなく1Hzの面影はありますが、もはや何Hzが重なっているのか判別不可能です。
でも周波数領域では相変わらず分かりやすいですね。
この波の性質で面白いのは、フリーハンドで描いたようなテキトーな波でも複数の波の重ね合わせで表現できることです。
図4-3 
図4-3の時間領域はフリーハンドで描いた波形です。周波数領域を見るとたくさんの周波数の波で構成されているのが分かります。
図4-4 
ちなみに実際の測定では、もっと細かく周波数が見れるので棒ではなく、各周波数バーのエッジを繋げた状態で表示されることもあります。
5.高い周波数の持つ意味
よくどのくらいの高さの周波数まで収録されているか?ということが話題になりますが、なぜ高い周波数を気にするのでしょうか?
高い周波数が持つ意味は何でしょうか?
それを探るために下図は図4-3と同じ波形ですが、高い周波数をどんどん削ってみたいと思います。
図5-1 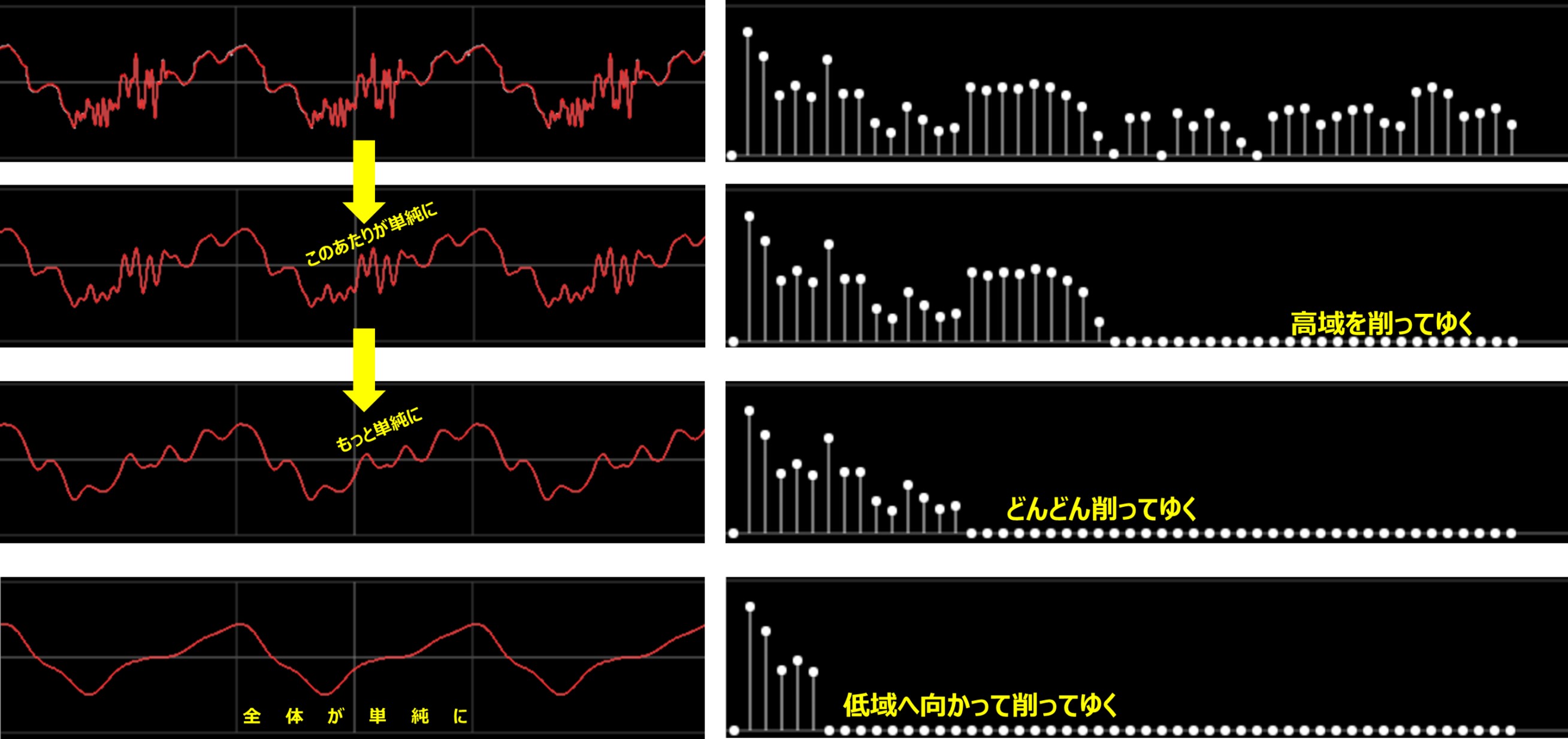
図5-1で上から順に時間領域に起こる変化を見てみると、まず真ん中の複雑なあたりがどんどん単純化してゆきます。
この真ん中の複雑なあたりは高い周波数によって出来ているのです。一番下では全体が単純になっています。
つまり元の波形のディティールを正確に保つには高い周波数の波が必要になるわけです。
図5-2 
ちなみに最後の1本まで削ると図3-2と同じような1Hzになります。逆に見ると最初の波形は1Hzに高周波数の波を足して出来ていたとも見れます。
実際の音楽を聴くうえで高い周波数は、楽器の明瞭さ、キラッとした感じや、クリアな感じ、
残響による空気間や空間の広がりを表現するうえで重要な要素です。
また、歌やアナウンスにおいても「ス」や「ツ」は一瞬の高周波で構成されており、
ここが収録されていないと「ス」か「ツ」かまたは「ウ」なのかの判別が難しくなります。
図5-3 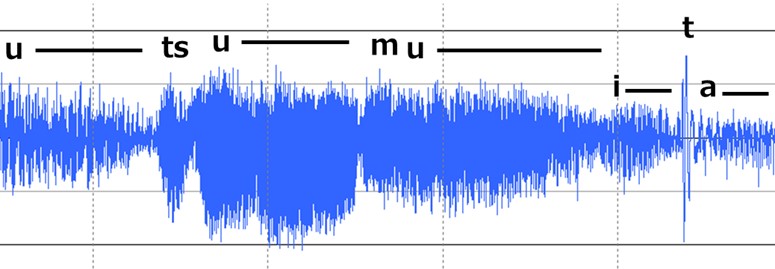
図5-3は「雨に消えたジョガー」の ♪うつむいた の時間領域表示です。
日本語はごく短い時間の子音と長めの母音が順番に出てくるような構成をしています。
tsuのところを拡大して見ると、
図5-4 
uは波が見え始めているのに対し、tsはまだクチャっとしているので、tsのほうが波が細かい、つまり高い周波数成分が多いことが分かります。
図5-5 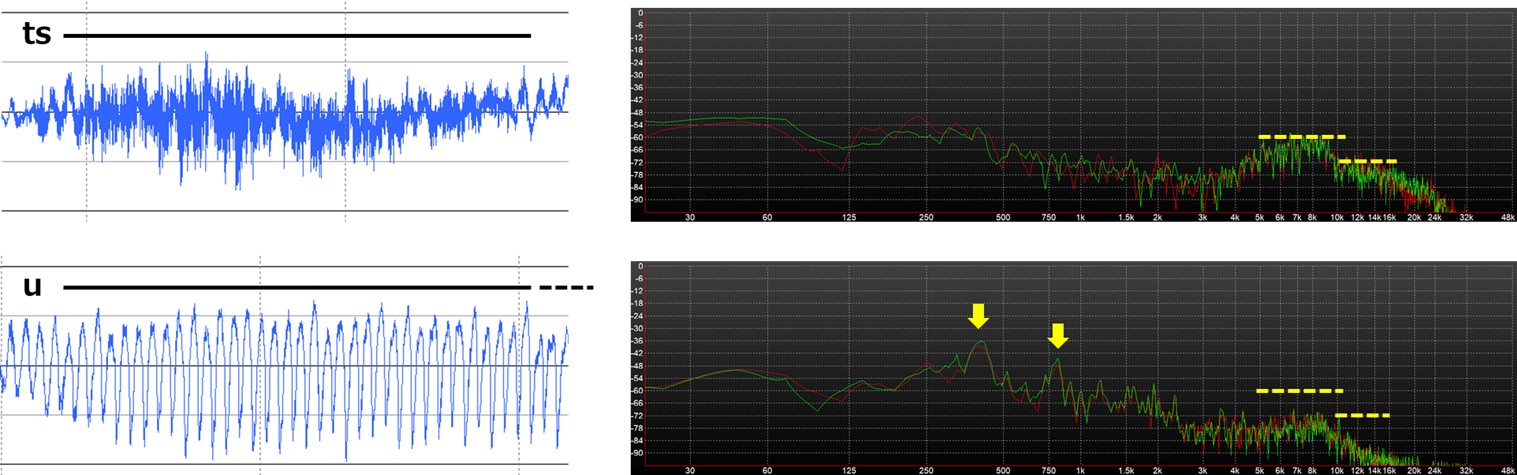
tsとuそれぞれの周波数領域を見てみると、tsのほうが4k-24(黄色破線のあたり)にわたって大きく収録されているのが分かります。
(なお、この周波数領域は棒が描かれていません。図4-4のような各棒の先を線でつないだ描き方と考えてください。)
uのほうは高域が小さい代わりに、黄色矢印で示した低めの周波数にピークがあり、この周波数が大きめの波を形作っています。
♪ううむいた ではなく ♪うつむいた と再生するためには高周波が必要なわけです。
ただし、LPやテープ系はCDと違いこの高さ(まぁ10kHz以上と言われてるようです)の音を上手く収録できないという難点もあるようですね。
また、人間は16kHz以上を空気伝搬ではほとんど聴き取れないと言われています
(ヘッドフォンでの聴取実験では能力の中い人で22kHzくらいが限界だそう)。
オーディオに置いてこの約20kHz以上を聴く必要があるのか/ないのか、いまだ議論が分かれているところのようです。
6. 歪むとどうなるか
大きすぎる音やレコードにおいては高すぎる周波数が音を歪ませてしまいます。音が歪むときは何が起こっているのでしょうか?
図6-1は図3-2と同じものですが、この信号を歪ませてみます。
図6-1 
まずは大きすぎる音による歪みです。
図6-2 
音が大きすぎて歪むとき、波の山と谷がちょん切られたような形になります。
このとき周波数領域では元々なかったはずの高い周波数が勝手に現れます。
次にレコード針が高い周波数を上手くトレースできない場合。
図6-3 
高い周波数と言いつつ、同じ周波数で描きますが、恐らく谷部分が上手くトレースできず、このような波形になると思います。
やはり勝手に高周波が発生します。
波が突然カクっと折れ曲げられてしまうとき、高周波が発生してしまいます。逆に言うと、
こういう急激な変化は高周波がないと構成できないのです。
この勝手な高周波が我々にはあの嫌な歪み音に聴こえるようです。
ただし、ギターのディストーションや残響なども歪みが生じている(元はなかったはずの音が付加される)ので、
一概に歪み=悪ではないのがややこしいところです。